Dai campi sulle sponde del Nilo
Un percorso storico-narrativo di
geometria come palestra di ragionamento per il biennio della scuola
superiore.
Premessa metodologica
Se sfogliamo le
prime pagine di un qualsiasi libro di geometria, troviamo che essa trae
la sua origine dall’esigenza pratica di ristabilire i confini dei campi
dei contadini dopo le periodiche inondanzioni del Nilo; è quanto
ci tramanda lo storico Erodoto. L’informazione si limita ad un semplice
aneddoto; dopo di che si “gira pagina” e si inizia con teoremi,
definizioni, anche con precisazioni pedanti (si dice “congruenti” e non
“uguali”, ecc....) che recide i legami con questa motivazione iniziale.
Da tempo abbiamo sperimentato un approccio costruttivo alla teoria,
adottando l'ipotesi dello Zeuthen, secondo cui fu il desiderio di
giustificare il teorema di Pitagora a condurre i geometri greci a
costruire catene di proposizioni, risalendo alle più evidenti (i
postulati, con un processo di analisi) per poi ridiscendere per
deduzione al teorema di Pitagora (sintesi). In seguito, per
aumentare il coinvolgimento degli studenti, abbiamo provato a sostenere
il percorso con una componente narrativa, cioè a svolgere un
compito in azione, in un contesto storico verosimile, identificandoci
nei ruoli dei protagonisti, cioè nei personaggi coinvolti nella
ridefinizione dei confini dei campi inondati dal Nilo; in particolare
in un gruppo di contadini coi campi confinanti e in uno scriba, o
notaio, che deve convincere con certezza e autorevolezza della
bontà dei suoi metodi per mettere d’accordo gli interessi
contrapposti dei contadini.
Gli agrimensori egizi erano chiamati "arpedonapti",
annodatori di funi,
essi compivano le operazioni concrete corrispondenti agli assiomi
euclidei:
- Tendendo una fune tra due punti, “tiravano” rette
- Prolungavano le "rette" limitate quando necessario
- Tenendo ferma la fune in un estremo, e tenendola tirata,
descrivevano circonferenze
Riportando su carta, in scala, la situazione dei campi, usiamo gli
strumenti più idonei, ma equivalenti, della riga e del compasso.
Sintesi del percorso
"Un contadino egiziano, Nilus, proprietario di un campo di forma
quadrata, eredita alla morte del padre un altro campo, sempre di forma
quadrata; con l'aiuto di uno scriba e di alcuni arpedonapti,
desidera riunire i due appezzamenti, piuttosto distanti, in un unico
campo, ancora di forma quadrata, che potrà coltivare più
agevolmente. Se tu fossi lo scriba, che istruzioni daresti agli
arpedonapti? Osservando il nuovo campo, Nilus non è convinto che
la nuova superficie sia proprio la somma delle precedenti; in che modo
cercheresti di convincerlo?"
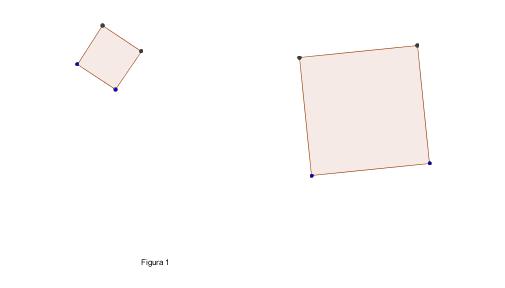
Occorre riportare, con le funi, un quadrato con un lato adiacente
all'altro, e applicare (figura 2) o scoprire (figura 3) il teorema di
Pitagora.
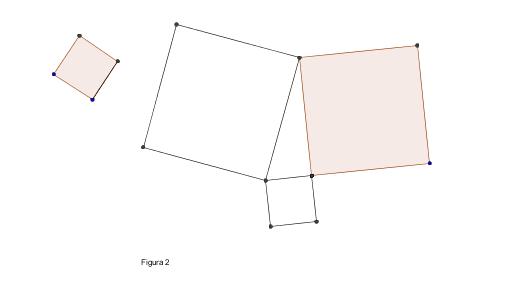
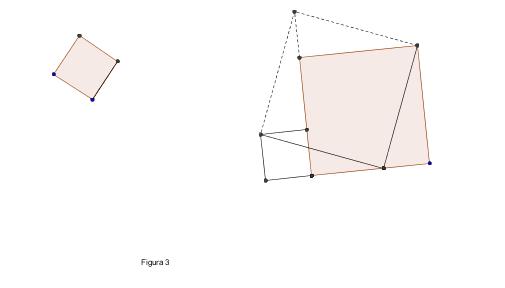
Ma come si costruisce un quadrato? Perché si ottiene proprio un
quadrato? Come si convince il contadino Nilus?
La costruzione del quadrato ripercorre
- la geometria “assoluta” (criteri di uguaglianza dei triangoli)
- la storia della geometria (quadrilatero di Saccheri)
- Va 'al cuore' della geometria euclidea nei suoi aspetti di tipo
costruttivo, logico, culturale.
La riproposizione
del problema in laboratorio di informatica, con un opportuno
software libero di geometria
dinamica (
Geogebra), collega
in modo naturale l'argomento delle trasformazioni geometriche
(isometrie): non avendo a disposizione un compasso per il trasporto dei
segmenti, occorre esplicitare con quale trsformazione si colloca un
dato segmento in una posizione
voluta.
Bibliografia
M. Berni, L. d'Angelo “Da
Pitagora agli assiomi”, Insegnare, n.5, 1995;
M. Berni, "Dai campi sulle sponde del Nilo", Dossier Insegnare, n. 1,
2008.